时间序列预测：2025 年完整指南

什么是时间序列预测？

时间序列预测是商业、金融、供应链管理、生产和库存计划中最常用的数据科学技术之一。许多预测问题都涉及时间组成部分，因此需要外推时间序列数据，即时间序列预测。时间序列预测也是机器学习 (ML) 的一个重要领域，可以被视为监督学习问题。诸如 回归、神经网络、支持向量机、随机森林和 XGBoost 等 ML 方法可以应用于此。预测涉及采用在历史数据上拟合的模型，并使用它们来预测未来的观测结果。

时间序列预测是指预测或估计未来一段时间内的值。它需要开发基于先前数据的模型，并应用它们进行观测和指导未来的战略决策。

未来是根据已经发生的事情进行预测或估计的。时间序列 在观测结果之间增加了时间顺序依赖性。这种依赖性既是一种约束，也是一种结构，它提供了额外的信息来源。在我们讨论时间序列预测方法之前，让我们更仔细地定义时间序列预测。

时间序列预测是一种通过时间序列预测事件的技术。它通过分析过去的趋势来预测未来的事件，假设未来的趋势将与历史趋势相似。它被广泛应用于各个研究领域，包括各种应用：

• 天文学
• 商业计划
• 控制工程
• 地震预测
• 计量经济学
• 数理金融
• 模式识别
• 资源分配
• 信号处理
• 统计学
• 天气预报

时间序列预测从历史时间序列开始。分析师检查历史数据，并检查时间分解模式，例如趋势、季节性模式、周期性模式和规律性。组织内的许多领域，包括市场营销、财务和销售，都使用某种形式的时间序列预测来评估可能的技术成本和消费者需求。时间序列数据的模型可以有多种形式，并代表不同的随机过程。

时间序列模型

时间序列模型用于根据经过验证的历史数据预测事件。常见的类型包括 ARIMA、基于平滑和移动平均。并非所有模型都会为相同的数据集产生相同的结果，因此确定哪种模型最适合基于各个时间序列至关重要。

在预测时，重要的是要了解您的目标。为了缩小预测建模问题的具体范围，请询问有关以下方面的问题：

1. 可用数据量 — 更多数据通常更有帮助，为探索性数据分析、模型测试和调整以及模型保真度提供更多机会。
2. 预测所需的时间范围 — 较短的时间范围通常比更长的时间范围更容易预测，并且置信度更高。
3. 预测更新频率 — 预测可能需要随时间频繁更新，或者可能需要一次性完成并保持静态（随着新信息的可用，更新预测通常会产生更准确的预测）。
4. 预测时间频率 — 通常可以在较低或较高的频率下进行预测，这允许利用数据的降采样和升采样（反过来，这可以在建模时提供好处）。

时间序列分析 vs. 时间序列预测

虽然 时间序列分析 完全是关于理解数据集；预测完全是关于预测它。时间序列分析包括用于分析时间序列数据的方法，以便提取有意义的统计数据和数据的其他特征。时间序列预测是使用模型根据先前观察到的值来预测未来值。

预测建模的三个方面是

1. 样本数据：我们收集的描述我们问题的数据，其中输入和输出之间存在已知关系。
2. 学习模型：我们在样本数据上使用的算法，用于创建我们可以稍后重复使用的模型。
3. 进行预测：在我们不知道输出的新数据上使用我们学习的模型。

验证和测试时间序列模型

使时间序列预测具有挑战性的因素包括

• 时间序列的时间依赖性 - 线性回归模型的基本假设，即观测值是独立的，在这种情况下不成立。由于时间序列数据中的时间依赖性，时间序列预测不能依赖于通常的验证技术。为了避免有偏差的评估，训练数据集应包含在验证集中观测值之前发生的观测值。一旦我们选择了最佳模型，我们就可以将其拟合到整个训练集上，并在随后的单独测试集上评估其性能。
• 时间序列中的季节性 - 除了增加或减少的趋势外，大多数时间序列都具有某种形式的季节性趋势，即特定时间范围特有的变化。

时间序列模型在特定数据集上可能优于其他模型 — 在一种类型的数据集上表现最佳的模型可能不会在所有其他数据集上表现相同。

预测方法的类型

模型	用途
分解法	时间序列的解构
基于平滑	去除异常值以获得清晰的模式
移动平均	跟踪单一类型的数据
指数平滑	基于平滑的模型 + 指数窗口函数

时间序列预测的示例

时间序列预测的示例包括：预测特定产品跨季节的消费者需求；家庭供暖燃料来源的价格；酒店入住率；医院住院治疗；欺诈检测；股票价格。您可以通过存储或机器学习模型执行预测。

让我们探讨使用开源时序数据库 InfluxDB 的预测示例。

存储预测

这是一个 存储预测（在 Veritas Technologies）的用例示例，下图取自该示例

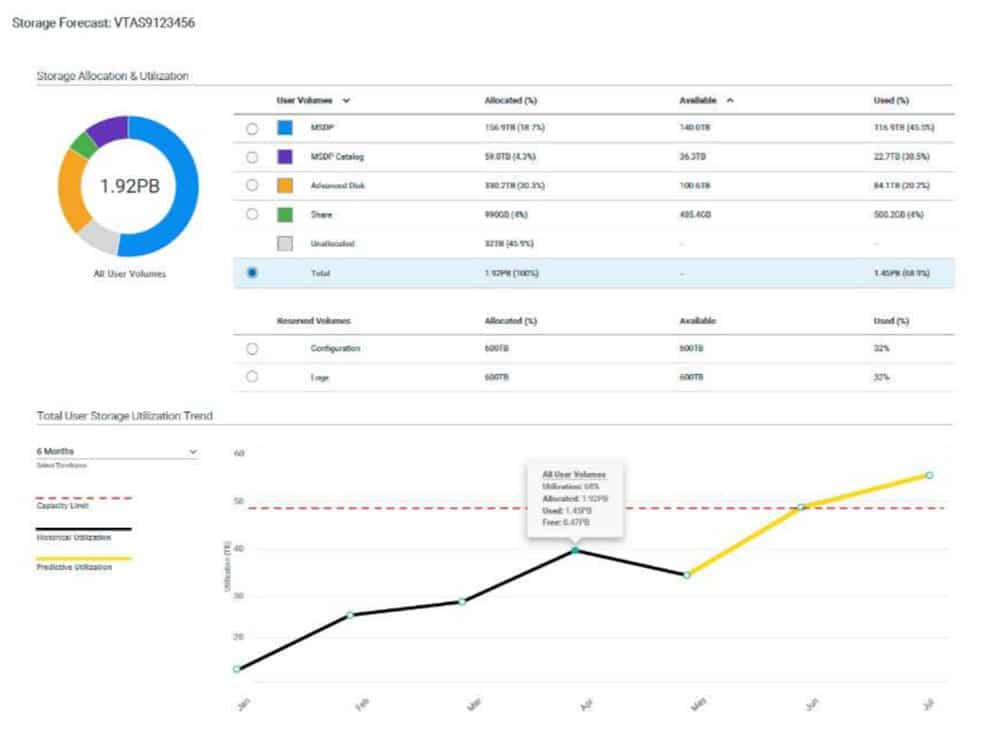
机器学习

这是一个机器学习（在 Playtech）的用例示例，下图取自该示例

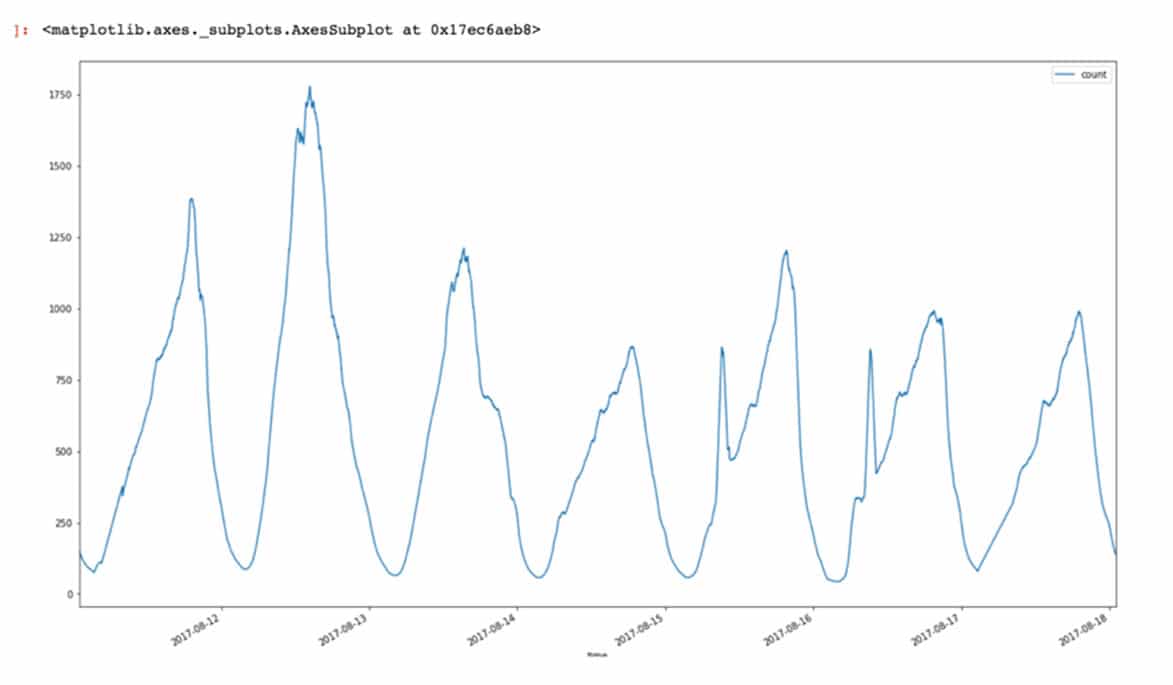
时间序列预测方法概述

分解模型

时间序列数据可以表现出各种模式，因此将时间序列分解为多个组成部分通常很有帮助，每个组成部分代表一个潜在的模式类别。这就是分解模型的作用。

时间序列的分解是一项统计任务，它将时间序列解构为几个组成部分，每个组成部分代表潜在的模式类别之一。当我们把时间序列分解成几个组成部分时，我们认为一个时间序列包含三个组成部分：趋势组成部分、季节性组成部分和残差或“噪声”（包含时间序列中的任何其他内容）。

主要有两种 分解类型：基于变化率的分解和基于可预测性的分解。

基于变化率的分解

这是一种重要的时间序列分析技术，尤其适用于 季节性调整。它旨在从观察到的时间序列中构建多个组成部分序列（可用于通过加法或乘法重建原始序列），其中每个序列都具有某种特征或行为类型。

如果数据显示出一些季节性（例如，每日、每周、每季度、每年），则将原始时间序列分解为三个组成部分的和可能很有用

Y(t) = S(t) + T(t) + R(t)

其中 S(t) 是季节性成分，T(t) 是趋势-周期成分，R(t) 是剩余成分。

有几种技术可以估计这种分解。最基本的一种称为经典分解，包括：

1. 通过滚动平均估计趋势 T(t)
2. 计算 S(t) 作为每个季节（例如，每个月）的平均去趋势序列 Y(t)-T(t)
3. 将剩余序列计算为 R(t)=Y(t)-T(t)-S(t)

时间序列也可以分解为

• T_t，时间 t 的趋势成分，反映了序列的长期发展趋势。当数据中存在持续的增加或减少方向时，就会出现趋势。
• C_t，时间 t 的周期性成分，反映了重复但非周期性的波动。这些波动的持续时间通常至少为两年。
• S_t，时间 t 的季节性成分，反映了季节性（季节性变化）。季节性发生在固定且已知的时间段内（例如，一年中的季度、月份或一周中的一天）。
• I_t，时间 t 的不规则成分（“残差”或“噪声”），描述了随机的、不规则的影响。

加法分解 vs. 乘法分解

在加法时间序列中，各成分相加构成时间序列。在乘法时间序列中，各成分相乘构成时间序列。

这是一个使用加法模型的时间序列示例

当趋势周围的变化不随时间序列的水平变化时，使用加法模型。要了解更多关于基于加法模型预测时间序列数据的信息，其中非线性趋势与年度、每周和每日季节性以及节假日效应相吻合，请参阅“使用 FB Prophet 和 InfluxDB 进行预测”教程，其中展示了如何进行单变量时间序列预测（Facebook Prophet 是 Facebook 发布的一个开源库，它基于可分解模型 — 趋势+季节性+节假日）。

这是一个使用乘法模型的时间序列示例

如果趋势与时间序列的水平成比例，则乘法模型是合适的。

基于可预测性的分解

时间序列分析理论利用了将时间序列分解为确定性成分和非确定性成分（或可预测成分和不可预测成分）的思想。

在统计学中，Wold 分解或 Wold 表示定理，以 Herman Wold 的名字命名，指出每个协方差平稳时间序列都可以写成两个时间序列之和，一个确定性的和一个随机性的。形式上

其中

• Y_t 是正在考虑的时间序列，
• E_t 是一个不相关的序列，它是该过程的创新过程 — 也就是说，一个输入到线性滤波器 {b_j} 的白噪声过程
• b 是移动平均权重（系数或参数）的可能无限向量
• n_t 是确定性时间序列，例如正弦波表示的时间序列。

用于预测的时间序列方法类型

时间序列方法指的是测量定时数据的不同方法。常见的类型包括：- 自回归 (AR) - 移动平均 (MA) - 自回归移动平均 (ARMA) - 自回归积分移动平均 (ARIMA) - 季节性自回归积分移动平均 (SARIMA)

重要的是根据时间序列数据的特征选择合适的预测方法。

基于平滑的模型

在时间序列预测中，数据平滑是一种统计技术，涉及从时间序列数据集中删除异常值，以使模式更清晰可见。在随时间收集的数据中，固有地存在某种形式的随机变化。平滑数据可以消除或减少随机变化，并显示潜在的趋势和周期性成分。

移动平均模型

在时间序列分析中，移动平均模型 (MA 模型)，也称为移动平均过程，是建模单变量时间序列的常用方法。移动平均模型指定输出变量线性依赖于随机（不完全可预测）项的当前值和各种过去值。

与自回归 (AR) 模型（下文介绍）一起，移动平均模型是更通用的时间序列 ARMA 和 ARIMA 模型的特例和关键组成部分，这些模型具有更复杂的随机结构。

与 AR 模型相反，有限 MA 模型始终是平稳的。

指数平滑模型

指数平滑是一种经验法则技术，用于使用指数窗口函数平滑时间序列数据。指数平滑是一种易于学习且易于应用的程序，可以根据用户的先前假设（例如季节性）进行一些确定。不同类型的指数平滑包括单指数平滑、双指数平滑和三指数平滑（也称为 Holt-Winters 方法）。有关如何开箱即用地将 Holt-Winters 与 InfluxDB 一起使用的教程，请参阅“当您想要 Holt-Winters 而不是机器学习时”和“使用 InfluxDB 预测下一次灭绝事件”）。

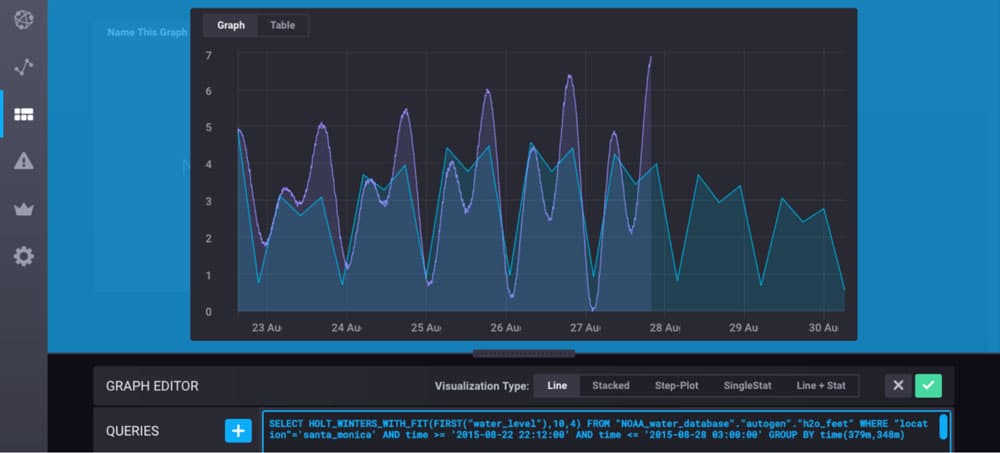
在单指数平滑中，预测由下式给出：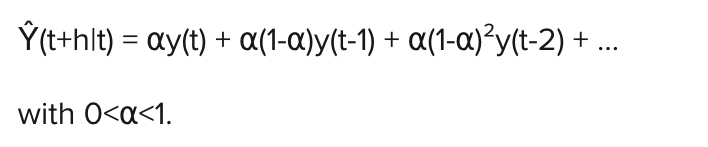

三指数平滑或 Holt Winters 在数学上与单指数平滑相似，只是季节性和趋势都包含在预测中。

移动平均模型 vs. 指数平滑模型

• 虽然在简单移动平均中，过去的观测值被赋予相同的权重，但指数函数用于随时间分配指数递减的权重（最近的观测值在预测中比旧的观测值被赋予相对更高的权重）。
• 在移动平均的情况下，分配给观测值的权重是相同的，并且等于 1/N。然而，在指数平滑中，有一个或多个平滑参数需要确定（或估计），这些选择决定了分配给观测值的权重。

包括季节性的预测模型

ARIMA 和 SARIMA

为了定义 ARIMA 和 SARIMA，首先定义自回归是有帮助的。自回归是一种时间序列模型，它使用先前时间步的观测值作为回归方程的输入，以预测下一个时间步的值。

自回归积分滑动平均 (ARIMA) 模型是最广泛使用的时间序列预测技术之一

• 在自回归模型中，预测值对应于变量过去值的线性组合。
• 在滑动平均模型中，预测值对应于过去预测误差的线性组合。

ARIMA 模型结合了上述两种方法。由于它们要求时间序列是平稳的，因此对时间序列进行差分（积分）可能是必要的步骤，即考虑差分的时间序列而不是原始时间序列。

SARIMA 模型（季节性 ARIMA）通过添加季节性过去值和/或预测误差的线性组合来扩展 ARIMA 模型。

TBATS

TBATS 模型是基于指数平滑的预测模型。该名称是三角 (Trigonometric)、Box-Cox 变换 (Box-Cox transform)、ARMA 误差 (ARMA errors)、趋势 (Trend) 和季节性 (Seasonal) 成分的首字母缩写。

TBATS 模型的主要特点是它能够处理多个季节性，通过使用基于傅里叶级数的三角表示来建模每个季节性。复杂季节性的一个经典例子是每日销售量的观测，这些观测通常具有每周和每年的季节性。